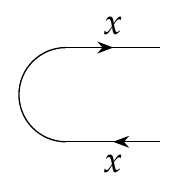
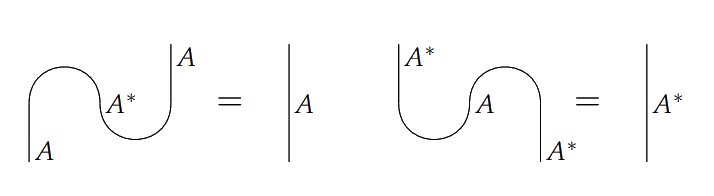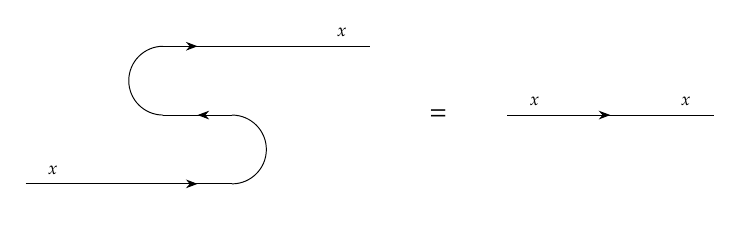![PDF] Dagger Compact Closed Categories and Completely Positive Maps: (Extended Abstract) | Semantic Scholar PDF] Dagger Compact Closed Categories and Completely Positive Maps: (Extended Abstract) | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/c69f4008fa5706f0b0acdf045bcefdef9fa697f8/18-Table2-1.png)
PDF] Dagger Compact Closed Categories and Completely Positive Maps: (Extended Abstract) | Semantic Scholar

Dagger Compact Closed Categories and Completely Positive Maps – topic of research paper in Computer and information sciences. Download scholarly article PDF and read for free on CyberLeninka open science hub.
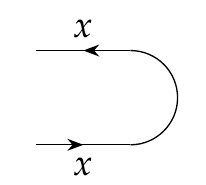
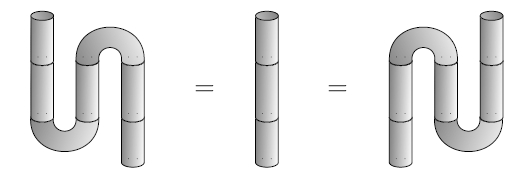
FINITE DIMENSIONAL HILBERT SPACES ARE COMPLETE FOR DAGGER COMPACT CLOSED CATEGORIES 1. Introduction Hasegawa, Hofmann, and Plotk

Non compact (2+1)-TQFTs from spherical non semisimple categories (Nathan Geer): Laboratoire Paul Painlevé - UMR 8524